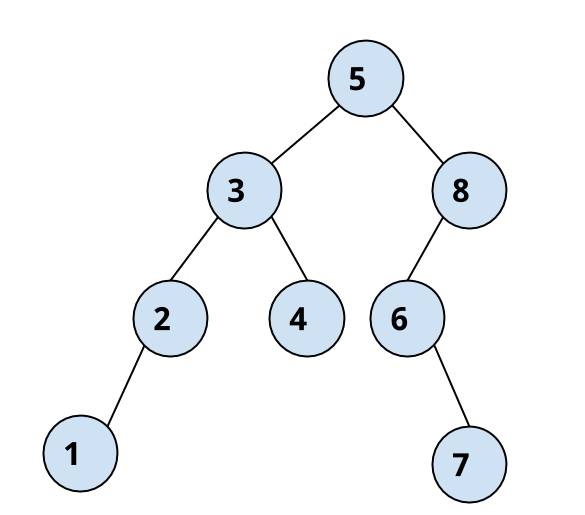
Given a binary tree, we have to print the data level wise.
For example level order traversal of the following tree produces the sequence 5,3,8,2,4,6,1,7.
The hint to solve this problem is to use a Queue data structure. We start by inserting the root node into the queue. Until the queue is empty, we remove the first element from the queue and insert it’s left and right children at the last.
This will give us the level order traversal of the binary tree. For example look at the queue state at each iteration.
5
3,8
8,2,4
2,4,6
4,6,1
…
Here is the C++ program which contains the level order traversal function.