Traversal algorithms of non-linear data structures like trees are designed to visit/print all the elements in that structure.
There are three main traversals of the binary tree. Namely
- In-order traversal
- Post-order traversal
- Pre-order traversal
In addition to these, there are inverses of the above algorithms, and there is a level order traversal.
In this post we will see the three main traversal algorithms mentioned above. All of these are defined as recursive algorithms.
In In-order traversal, we first visit the left sub-tree, then root, and then the right sub-tree.
In Post-order traversal, we first visit the left sub-tree, then the right sub-tree, and then the root.
In Pre-order traversal, We first visit the root, then visit the left sub-tree and then visit the right sub-tree.
For example consider the simple 3 node binary tree
In-order traversal: B A C
Post-order traversal: B C A
Pre-order traversal: A B C
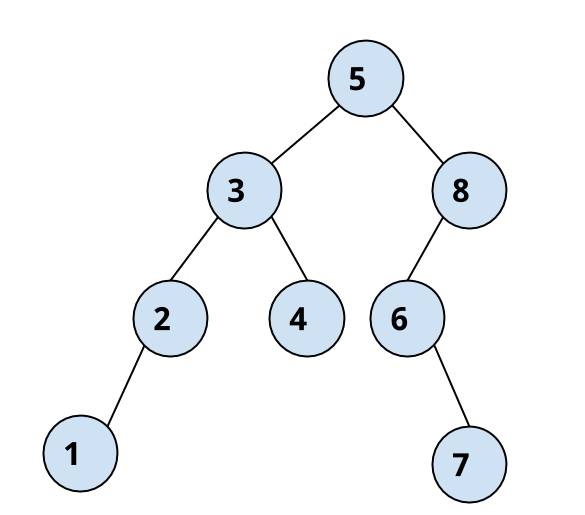
To consider a bigger example, take the following binary search tree and it’s traversal sequences for the three algorithms.
In-order: 1 2 3 4 5 6 7 8
Post-order: 1 2 4 3 7 6 8 5
Pre-order: 5 3 2 1 4 8 6 7
The in-order traversal of the binary search tree always produces the sorted order of it’s elements.
Here is the C++ code for all the traversals.