Given a number of unit squares (1 x 1). How many different rectangles can be formed with them?
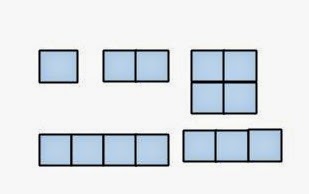
For example let us consider 4 units. We can form 5 different rectangles like the following. Two rectangles are considered same if they are oriented in a different way but same dimensions.
Basically we have to arrange 1 to N-1 units to form rectangles of different dimensions.
This boils down to finding the sum of the number of pairs factors of 1 to N numbers.
Here is the C++ program to do that.
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| #include <iostream> | |
| #include <cmath> | |
| using namespace std; | |
| int main() { | |
| int n; | |
| cin >> n; | |
| int i,j; | |
| int r = 0; | |
| for( i = 1; i <= n; i++ ) | |
| { | |
| for( j = 1; j <= sqrt(i*1.0); j++ ) | |
| { | |
| if( i % j == 0 ) | |
| r++; | |
| } | |
| } | |
| cout << r << endl; | |
| return 0; | |
| } |
 by
by