Given only pre-order and post order traversals, we can not construct a unique binary tree from them.
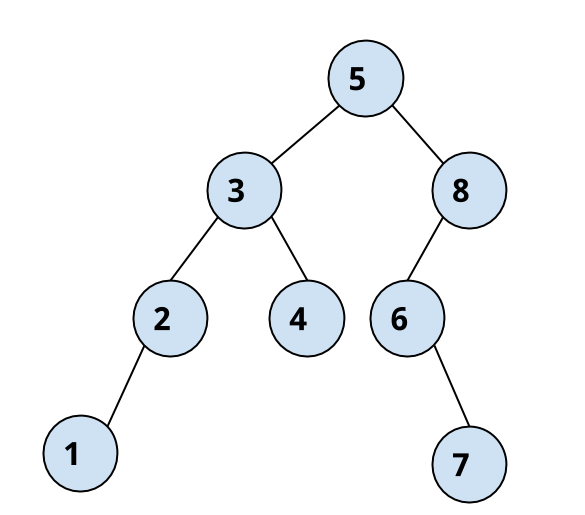
For example given
In-order : {1, 2, 3, 4, 5, 6, 7, 8}
Pre-order: {5, 3, 2, 1, 4, 8, 6, 7}
We have to create the following binary tree
We use recursive approach for constructing a binary tree from In-order and Post-order or Pre-order traversals .
Constructing from Inorder and Preorder:
In Pre order, we first traverse the root, then left sub tree and right sub tree. So the first element in the pre order is always the root. We search for this element in the in-order sequence. This index divides the in-order sequence into left subtree and right subtree.
For example consider the following binary tree
1
/
2 3
/ /
4 5 6 7
Inorder: {4, 2, 5, 1, 6, 3, 7}
Preorder: {1, 2, 4, 5, 3, 6, 7}
Create 1 as the root node,
- all the left elements to the left of it {4, 2, 5} form the left subtree
- all the elements to the right of it {6, 3, 7} form the right subtree
We can use the index of 1 in Inorder (in this case 3) to calculate the size of the left and right subtrees.
Size(left subtree) = index
Size(right subtree) = size-index-1
We can also use this index to calculate the offset of Inorder and Post order sequences for the subtree.
To create the left subtree we pass Inorder:{4, 2, 5} Preorder:{2, 4, 5} as parameters to the recursive call.
To create the right subtree we pass Inorder:{6, 3, 7} Preorder:{3, 6, 7} as parameters.
Constructing from Inorder and Postorder:
In post order, we first traverse the left subtree, right subtree and visit the root. So the last element in the post order sequence is the root.
Similar to the above algorithm, this element divides the in-order sequence into left subtree and right subtree.
Considering the same example as above the Post order is {4, 5, 2, 6, 7, 3, 1}
Once we create the root with the last element i.e 1.
We pass the following parameters to create the left and right subtrees.
Inorder Postorder
Left Subtree {4, 2, 5} {4, 5, 2}
Right Subtree {6, 3, 7} {6, 7, 3}
Here is the C++ implementation of the above two algorithms.
| #include <iostream> | |
| #include <queue> //for level order traversal | |
| #include <algorithm> //find algorithm | |
| using namespace std; | |
| struct TreeNode | |
| { | |
| int val; | |
| TreeNode *left, *right; | |
| TreeNode(int v):val(v),left(NULL), right(NULL) | |
| { | |
| } | |
| }; | |
| //Given inorder and pre order traversals, this method returns the | |
| //root of the binary tree node constructed from them | |
| TreeNode* makeBinTreeFromInPre(int inorder[], int preorder[], int size) | |
| { | |
| TreeNode* root = NULL; | |
| if( size == 0 ) // empty tree | |
| return NULL; | |
| root = new TreeNode( preorder[0] ); | |
| int *ptr = find( inorder, inorder+size, preorder[0] ); | |
| int index = ptr - inorder; | |
| root->left = makeBinTreeFromInPre(inorder, preorder+1, index); | |
| root->right = makeBinTreeFromInPre(inorder+index+1, preorder+index+1, size-index-1); | |
| return root; | |
| } | |
| //Given inorder and post order traversals, this method returns the | |
| //root of the binary tree node constructed from them | |
| TreeNode* makeBinTreeFromInPost(int inorder[], int postorder[], int size) | |
| { | |
| TreeNode* root = NULL; | |
| if( size == 0 ) // empty tree | |
| return NULL; | |
| root = new TreeNode( postorder[size-1] ); | |
| int *ptr = find( inorder, inorder+size, postorder[size-1] ); | |
| int index = ptr - inorder; | |
| root->left = makeBinTreeFromInPost(inorder, postorder, index); | |
| root->right = makeBinTreeFromInPost(inorder+index+1, postorder+index, size-index-1); | |
| return root; | |
| } | |
| //prints the nodes in Binary tree in level order fashion. | |
| void printLevelOrder( TreeNode* root ) | |
| { | |
| if( root == NULL ) | |
| { | |
| return; | |
| } | |
| queue<TreeNode*> q; | |
| q.push(root); | |
| while( !q.empty() ) | |
| { | |
| TreeNode * temp = q.front(); | |
| q.pop(); | |
| cout << temp->val << " "; | |
| if( temp->left != NULL ) | |
| q.push(temp->left); | |
| if( temp->right != NULL ) | |
| q.push(temp->right); | |
| } | |
| cout << endl; | |
| } | |
| void test1() | |
| { | |
| int inorder[] = {4, 2, 5, 1, 3}; | |
| int preorder[] = {1, 2, 4, 5, 3}; | |
| TreeNode * root = makeBinTreeFromInPre(inorder, preorder, 5); | |
| printLevelOrder(root); | |
| } | |
| void test2() | |
| { | |
| int inorder[] = {4, 2, 5, 1, 3}; | |
| int postorder[] = {4, 5, 2, 3, 1}; | |
| TreeNode * root = makeBinTreeFromInPost(inorder, postorder, 5); | |
| printLevelOrder(root); | |
| } | |
| void test3() | |
| { | |
| int inorder[] = {3, 2, 1, 4, 5}; | |
| int preorder[] = {1, 2, 3, 4, 5}; | |
| TreeNode * root = makeBinTreeFromInPre(inorder, preorder, 5); | |
| printLevelOrder(root); | |
| } | |
| void test4() | |
| { | |
| int inorder[] = {3, 2, 1, 4, 5}; | |
| int postorder[] = {3, 2, 5, 4, 1}; | |
| TreeNode * root = makeBinTreeFromInPost(inorder, postorder, 5); | |
| printLevelOrder(root); | |
| } | |
| void test() | |
| { | |
| test1(); | |
| test2(); | |
| test3(); | |
| test4(); | |
| } | |
| int main() | |
| { | |
| test(); | |
| return 0; | |
| } |
 by
by