Finding the height of the binary tree

Given a binary tree how to find the height of the tree.

It is defined as the number of nodes in the longest path from root to any leaf.

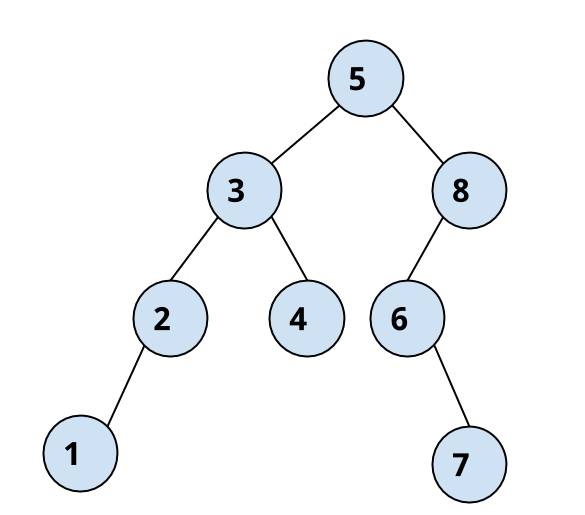
We can assume that the height of empty tree is 0 and the height of a tree with just root node as 1. For example the below tree has a height of 4.

We can calculate the height of the tree using recursive method very easily. It is based on the observation that height of a binary tree is

1 + Max( height(left-sub-tree), height(right-sub-tree) )

Here is the C++ code which implements this simple algorithm.

	#include <iostream>

	using namespace std;

	class BSTNode
	{
	int data;
	BSTNode *left;
	BSTNode *right;

	public:
	//single param constructor
	BSTNode(int d):data(d), left(NULL), right(NULL)
	{
	}

	BSTNode(int d, BSTNode l, BSTNode r):data(d), left(l), right(r)
	{
	}

	int getData()
	{
	return data;
	}

	void setData(int d)
	{
	data = d;
	}

	BSTNode* getLeft()
	{
	return left;
	}

	void setLeft(BSTNode *l)
	{
	left = l;
	}

	BSTNode* getRight()
	{
	return right;
	}

	void setRight(BSTNode *r)
	{
	right = r;
	}

	};

	class BinarySearchTree
	{
	BSTNode * root;
	public:
	BinarySearchTree():root(NULL)
	{
	}
	BSTNode * getRoot()
	{
	return root;
	}
	bool insert(int d)
	{
	if( root == NULL ) // if tree is empty
	{
	root = new BSTNode(d);
	return true;
	}
	else
	{
	BSTNode *ptr = root;
	BSTNode *prev = NULL;

	while( ptr != NULL )
	{
	prev = ptr;

	if( ptr->getData() == d )//no duplicates allowed in BST
	return false;
	else if( ptr->getData() < d )
	{
	ptr = ptr->getRight();
	}
	else
	{
	ptr = ptr->getLeft();
	}
	}

	if( prev->getData() < d ) //to be added as right child?
	prev->setRight( new BSTNode(d) );
	else
	prev->setLeft( new BSTNode(d) );
	return true;
	}
	}

	int height(BSTNode *ptr)
	{
	if( ptr == NULL )
	return 0;
	else
	{
	return 1 + max( height(ptr->getLeft()), height(ptr->getRight()) );
	}
	}

	};

	int main()
	{
	BinarySearchTree *bst = new BinarySearchTree();

	bst->insert(5);
	bst->insert(3);
	bst->insert(8);
	bst->insert(4);
	bst->insert(9);
	bst->insert(1);
	bst->insert(10);
	bst->insert(2);
	bst->insert(6);
	bst->insert(7);

	cout << bst->height( bst->getRoot() ) << endl;

	return 0;
	}

by GitHub