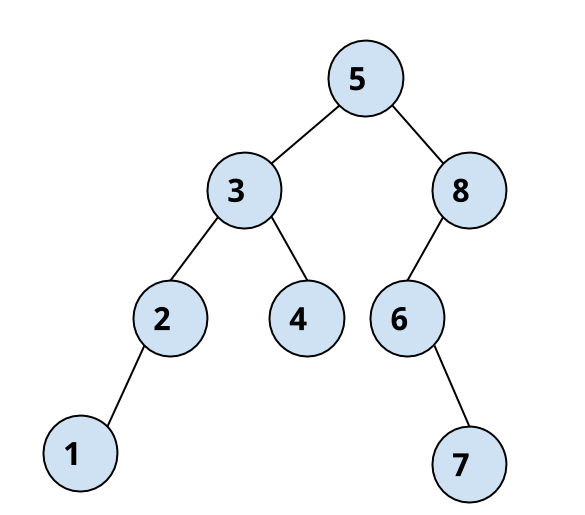
How to insert into a binary search tree

A binary search tree is a hierarchical data structure which stores data in a non-linear fashion. It supports the insertion, search and deletion operations in O( log n ) time. Take a look at the below picture.

This is an example of binary search tree. The node at the top containing 5 is the root and all the elements to the left of it(left sub-tree) are less than 5 and all the elements to the right of it (right sub-tree) are greater than 5. A binary search tree does not allow duplicate elements in it.

In this post we see how an insertion method works. It works very similar to the binary search.

The insert method looks at the root. If the given data is lesser than root data, it has to be inserted into the left sub-tree. Otherwise it has to be added in the right sub-tree. Since the left/right sub-trees are also binary search trees, we call the procedure recursively.

Here is the complete C++ program which implements a binary search tree in Object Oriented approach. I have used in-order traversal to print all the elements of the binary search tree. These procedures are explained in future posts.

	#include <iostream>

	using namespace std;

	//Define binary search tree node
	class BSTNode
	{
	int data;
	BSTNode *left;
	BSTNode *right;

	public:
	//single param constructor
	BSTNode(int d):data(d), left(NULL), right(NULL)
	{
	}

	BSTNode(int d, BSTNode l, BSTNode r):data(d), left(l), right(r)
	{
	}

	int getData()
	{
	return data;
	}

	void setData(int d)
	{
	data = d;
	}

	BSTNode* getLeft()
	{
	return left;
	}

	void setLeft(BSTNode *l)
	{
	left = l;
	}

	BSTNode* getRight()
	{
	return right;
	}

	void setRight(BSTNode *r)
	{
	right = r;
	}

	};

	//Define the binary search tree itself
	class BinarySearchTree
	{
	BSTNode * root;
	public:
	BinarySearchTree():root(NULL)
	{
	}
	BSTNode * getRoot()
	{
	return root;
	}
	bool insert(int d)
	{
	if( root == NULL ) // if tree is empty
	{
	root = new BSTNode(d);
	return true;
	}
	else
	{
	BSTNode *ptr = root;
	BSTNode *prev = NULL;

	while( ptr != NULL )
	{
	prev = ptr;

	if( ptr->getData() == d )//no duplicates allowed in BST
	return false;
	else if( ptr->getData() < d )
	{
	ptr = ptr->getRight();// go to right sub-tree
	}
	else
	{
	ptr = ptr->getLeft();// go to left sub-tree
	}
	}

	if( prev->getData() < d ) //to be added as right child?
	prev->setRight( new BSTNode(d) );
	else
	prev->setLeft( new BSTNode(d) );
	return true;
	}
	}

	//prints all the elements in binary tree in left - root - right order
	void inorder(BSTNode *root)
	{
	if( root )
	{
	inorder( root->getLeft() );
	cout<< root->getData() << " ";
	inorder( root->getRight() );
	}
	}

	};

	int main()
	{
	BinarySearchTree *bst = new BinarySearchTree();

	bst->insert(5);
	bst->insert(3);
	bst->insert(8);
	bst->insert(4);
	bst->insert(9);
	bst->insert(1);
	bst->insert(10);
	bst->insert(2);
	bst->insert(6);
	bst->insert(7);

	//in-order traversal should print the elements in ascending order
	bst->inorder( bst->getRoot() );

	cout << endl;

	return 0;
	}

view raw BinarySearchTree.cpp hosted with

by GitHub

Leave a Reply Cancel reply